Monte Carlo methods (or Monte Carlo experiments) are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in simulating physical and mathematical systems. Because of their reliance on repeated computation of random or pseudo-random numbers, these methods are most suited to calculation by a computer and tend to be used when it is unfeasible or impossible to compute an exact result with a deterministic algorithm.
Monte Carlo simulation methods are especially useful in studying systems with a large number of coupled degrees of freedom, such as fluids, disordered materials, strongly coupled solids, and cellular structures (see cellular Potts model). More broadly, Monte Carlo methods are useful for modeling phenomena with significant uncertainty in inputs, such as the calculation of risk in business. These methods are also widely used in mathematics: a classic use is for the evaluation of definite integrals, particularly multidimensional integrals with complicated boundary conditions. It is a widely successful method in risk analysis when compared with alternative methods or human intuition. When Monte Carlo simulations have been applied in space exploration and oil exploration, actual observations of failures, cost overruns and schedule overruns are routinely better predicted by the simulations than by human intuition or alternative "soft" methods.
The term "Monte Carlo method" was coined in the 1940s by physicists working on nuclear weapon projects in the Los Alamos National Laboratory.
There is no single Monte Carlo method; instead, the term describes a large and widely-used class of approaches. However, these approaches tend to follow a particular pattern:
1.Define a domain of possible inputs.
2.Generate inputs randomly from the domain using a certain specified probability distribution.
3.Perform a deterministic computation using the inputs.
4.Aggregate the results of the individual computations into the final result.
Although Monte Carlo methods are used in a dizzingly diverse number of ways, in the context of molecular computations there are five types most commonly encountered:
Different types of Monte Carlo method:
Classical Monte Carlo method:(CMC)
samples are drawn from a probability distribution, often the classical Boltzmann distribution, to obtain thermodynamic properties, minimum-energy structures and/or rate coefficients, or perhaps just to sample conformers as part of a global conformer search algorithm.
Quantum Monte Carlo method:(QMC)
random walks are used to compute quantum-mechanical energies and wave functions, often to solve electronic structure problems, using Schroedinger's equation as a formal starting point
Path Integral quantum Monte Carlo method:(PMC)
This method is a quantum statistical mechanical integrals which are evaluated at to obtain thermodynamic properties.
Kinetic Monte Carlo method:(KMC)
A set of algorithm that simulate a process based on various events with certain with certain rate occurrence used in reactions, etc.
Volumetric Monte Carlo, or VMC :
Random and quasirandom number generators are used to generate molecular volumes and sample molecular phase-space surfaces
Simulation Monte Carlo, or SMC:
Stochastic algorithms are used to generate initial conditions for quasiclassical trajectory simulations, or to actually simulate processes using scaling arguments to establish time scales or by introducing stochastic effects into molecular dynamics. "Kinetic Monte Carlo" is an example of an SMC method. So is "thermalization" of a molecular dynamics trajectory.
Examples using Monte Carlo method:
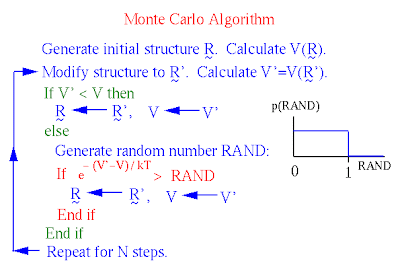
Instead of evaluating forces to determine incremental atomic motions, Monte Carlo simulation simply imposes relatively large motions on the system and determines whether or not the altered structure is energetically feasible at the temperature simulated. The system jumps abruptly from conformation to conformation, rather than evolving smoothly through time. It can traverse barriers without feeling them; all that matters is the relative energy of the conformations before and after the jump. Because MC simulation samples conformation space without a true `time' variable or a realistic dynamics trajectory, it cannot provide time-dependent quantities. However, it may be much better than MD in estimating average thermodynamic properties for which the sampling of many system configurations is important.
Monte Carlo makes use of Boltzmann probabilities, not forces.
When the potential energy V and observables to be calculated from the simulation are velocity-independent (as is typical), an MC simulation need only compare potential energies V, not total energies E (see `Calculating Equilibrium Averages' above). Two conformations, and , are compared and updated as shown below. is a random number uniformly distributed on {0,1}
Metropolis Monte Carlo.
For simple systems, the structural modifications are often tuned so that about 50% of the conformations are accepted. For macromolecular systems, this acceptance ratio can be much smaller, e.g. when dihedral angles are modified by large amounts. It is then generally expedient to bias the random moves in favor of known structural preferences such as side chain rotamers (`biased probability Monte Carlo'). In searching for low-energy local minima, it can be advantageous to minimize the energy before evaluating the energy (`Monte Carlo-minimization', or MCM ). Simulated annealing has also been performed prior to accepting or rejecting the new conformation in a `Monte Carlo-minimization/annealing' (MCMA) protocol. Because explicit water molecules can hinder the acceptance of new conformations, Monte Carlo (or MCM, MCMA) simulations of macromolecules generally use an implicit model of solvation, as in references . That is, a term is added to the empirical potential energy function that mimics the effects of water and, in some cases, counter ions.



No comments:
Post a Comment